第七节 t
检验和u 检验 (1)
(2) (3) (4)
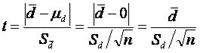 v=n-1 公式(10.26)
v=n-1 公式(10.26)
式中d为每对数据的差值,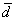 为差值的样本均数, 为差值的样本均数,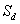 为差值的标准差, 为差值的标准差,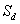 为差值样本均数的标准误,n为对子数。 为差值样本均数的标准误,n为对子数。
3. 两样本t 检验 亦称成组t 检验。用于完全随机设计的定量资料的两样本均数的比较,目的是推断两样本均数各自所代表的总体均数μ1和μ2是否相等。完全随机设计是指分别从两研究总体中随机抽取样本,然后比较两组的总体指标。
当两样本的总体方差相等(即方差齐)时,其检验统计量的计算公式为:
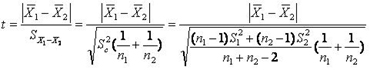 v=n1+n2-2 公式(10.27)
v=n1+n2-2 公式(10.27)
式中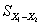 为两样本均数之差的标准误, 为两样本均数之差的标准误,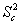 为两样本合并方差, 为两样本合并方差,
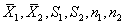 分别为两样本的均数、标准差、样本含量。 分别为两样本的均数、标准差、样本含量。
上述公式(10.27)只适用于满足方差齐性的两样本t检验,若方差不齐时,可采用近似t检验(亦称t’检验)(可参见相关的参考书)或后述的秩和检验。
二、u 检验
1. 单样本u 检验 常用于一组大样本(n>100)定量资料的样本均数代表未知的总体均数μ和已知的总体均数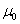 (一般为理论值、标准值或经大量观察所得的稳定值)进行比较。其检验统计量的计算公式为:
(一般为理论值、标准值或经大量观察所得的稳定值)进行比较。其检验统计量的计算公式为:
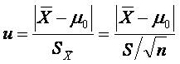 公式(10.28)
公式(10.28)
上述公式(10.28)实际上是当n>100时,单样本t检验的公式(10.25)的近似式。
当σ已知时,只把公式(10.28)中的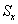 换成 换成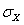 即可,但此公式很少用。 即可,但此公式很少用。 |
|


