第五节 多服务台模型(M/M/C)    (1) (2) (3) (4) (5) (6)
    例5 某单位电话交换台有一台200门内线的总机。已知在上班的八小时内，有20%的内线分机平均每四十分钟要一次外线电话，80%的分机平均隔两小时要一次外线电话，又知从外单位打来的电话呼唤平均每分钟一次，设外线通话时间平均三分钟，以上两个时间均属负指数分布。如果要求电话接通率为95%，问该交换台应设置多少外线？
    解：⑴来到电话交换台的呼唤有两类：一是各分机往外打的电话，二是从外单位打进来的电话。
    前一类λ1 =（0.2×60/40+0.8×1/2）×200=140（次/小时）后一类λ2 =60（次/小时）
    根据普阿松分布的性质，来到交换台的总呼唤流仍为普阿松流，其参数λ=λ1+λ2=200。
    ⑵这是一个具有多个服务台带损失制的服务系统，要使电话接通率为95%，就要使损失率低于5%，亦即
        
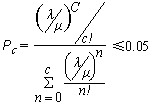
    问题中μ=60/3=20（次/小时）, λ/μ=200/20=10,可以通过列表计算,来求得满足要求的C。
        
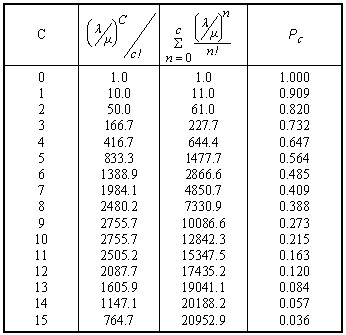
    根据上表计算结果可以看出，要使外线接通率达95%，交换台应设置不少于15条的外线。
    说明：①计算中没有考虑外单位打来电话时，内线是否占用，也没有考虑分机打外线时，对方是否占线。
    ②当电话一次打不通时，就要打两次、三次、…，因此实际呼唤次数要远远高于计算次数，因此实际接通率也要比95%低得多。