第五节 多服务台模型(M/M/C)    (1) (2) (3) (4) (5) (6)
    例6 设有三名工人负责照管20台自动机床。当机床需要加料、发生故障或刀具磨损时，就自动停车，等待工人照管。设平均每台机床每小时停车一次，又设每台机床停车时，需要工人平均照管的时间为0.1小时。以上两项时间均服从负指数分布，试计算该系统的各项指标。
    解：这里C=3，m=20，λ/μ=0.1,列表计算如下：
        
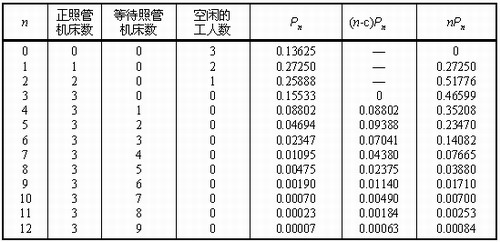
    因为n＞12时，Pn＜0.5×10-5,故忽略不计。由上表计算的数值可得：
    系统中平均等待工人照管的机床数
    Lq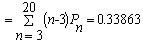
    停车的机床总数（包括正在照管与等待照管数）
    Ls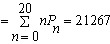
    有效到达率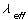 =λ(m-Ls)=20-2.12677=17.87323
    逗留时间 Ws=Ls/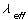 =2.12677÷17.87323=0.12（小时)
    Wq=Ws-1/μ=0.12-0.1=0.02（小时）