二、传递函数的性质

从线性定常系统传递函数的定义式(2.23)可知，传递函数具有以下性质：

1.传递函数是复变量s的有理真分式函数，分子的阶数m小于或等于分母的阶数n （m≤n） ，且所有系数均为实数。

2.传递函数只取决于系统和元件的结构和参数，与外作用及初始条件无关。

3.传递函数的零、极点分布图也表征了系统的动态性能。将式(2.23)中分子多项式及分母多 项式因式分解后，写为如下形式：

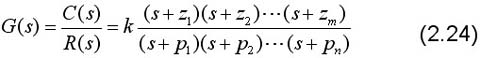
式中k为常数，-z1,…,-zm为传递函数分子多项式方程的m个根，称之为传递函数的零点；-p1,…,-pn为分母多项式方程的n个根，称为传递函数的极点。

一般zi，pi可以为实数，也可为复数，且若为复数，必共轭成对出现。将零、极点标在复平面上，则得到传递函数的零极点分布图，如图2-7所示。

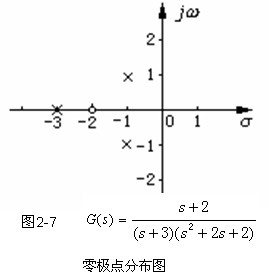
图中零点用“o”表示，极点用“X ”表示。

4. 若令式(2.23)中s = 0，则：

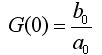
常称为传递系数（或静态放大系数）。从微分方程式(2.22)看，s=0相当于所有导数项为零，方程变为静态方程:

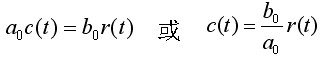
b0 /a0为输出输入的静态比。

5. 传递函数无法全面反映信号传递通路中的中间变量。多输入多输出系统各变量间的关系要用传递函数阵表示。

三、典型环节及其传递函数

控制系统从动态性能或数学模型来看，可分成为以下几种基本环节，也就是典型环节。

（一）比例环节

比例环节的传递函数为：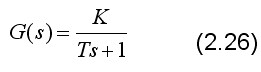

输出量与输入量成正比，比例环节又称为无惯性环节或放大环节。

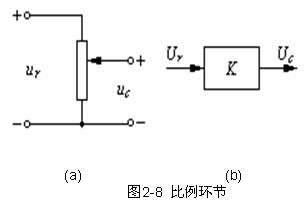
图2-8(a)所示为一电位器，输入量和输出量关系如图2-8(b)
所示。

（二）惯性环节

传递函数为如下形式的环节为
惯性环节：

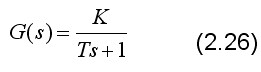
式中 K——环节的比例系数；
T——环节的时间常数。

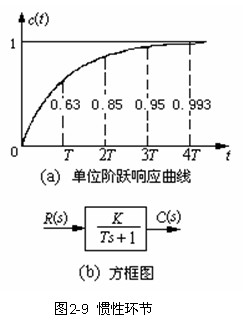
当环节的输入量为单位阶跃函数时，
环节的输出量将按指数曲线上升，
具有惯性，如图
2-9(a)所示。

（三）积分环节

它的传递函数为: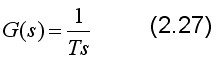

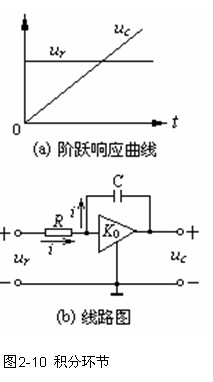
当积分环节的输入为单位阶跃函数时，
则输出为t/T，它随着时间直线增长。
T称为积分时间常数。T很大时惯性环节的
作用就近似一个积分环节。

图2-10(b)为积分调节器。 积分时间
常数为RC。

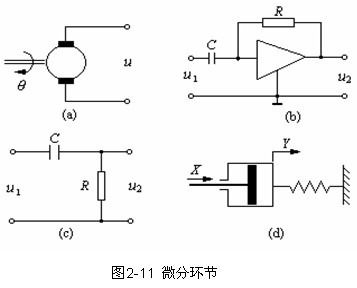
（四）微分环节

理想微分环节传递函数为: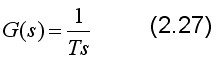

输入是单位阶跃函数1(t)时，理想微分环节的输出为c(t)=Td(t)， 是个脉冲函数。
理想微分环节的实例示于图2-11(a)、(b)。(a)为测速发电机。图2-11(b)为微分运算放大器。

在实际系统中，微分环节常带有惯性，它的传递函数为：

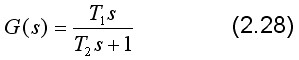
它由理想微分环节和惯性环节组成，如图2-11(c)、(d)所示。在低频时近似为理想微分环节，否则就有式(2.28)的传递函数。

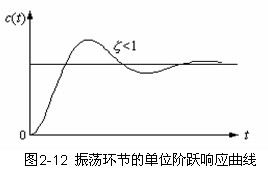
（五）振荡环节

振荡环节的传递函数为：

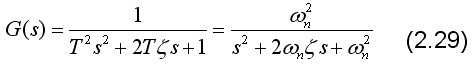
式中ψn ---无阻尼自然振荡频率，ψn=1/T；ζ ——阻尼比，0＜ζ＜1。

图2-12所示为单位阶跃函数作用下的响应曲线。

延滞环节的传递函数可求之如下：c(t)= r(t-τ)

其拉氏变换为:

式中ξ = t-τ，所以延滞环节的传递函数为:

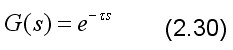
系统具有延滞环节对系统的稳定性不利，延滞越大，影响越大。