求系统的传递函数时，需要对微分方程组或拉氏变换后的代数方程组进行消元。而采用结构图或信号流图，更便于求取系统的传递函数，还能直观地表明输入信号以及各中间变量在系统中的传递过程。因此，结构图和信号流图作为一种数学模型，在控制理论中得到了广泛的应用。

一 、控制系统的结构图

（一 ）结构图的概念

图2-14 RC网络的微分方程式为:

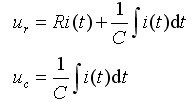
也可写为:

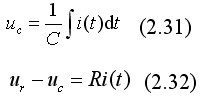
对上面二式进行拉氏变换，得:

将式(2.32a)表示成:

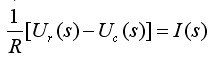
可由图2-15(a)描绘。将图2-15(a)、图2-15(b)，合并如图2-15(c)所示。

信号线： 带箭头的直线，箭头表示信号的传递方向，

引出点：表示信号引出或测量的位置，从同一点引出的信号在数值和性质方面
完全相同。

比较点：表示对信号进行加减运算。“+”号可以省略。

方 框：表示对信号进行数学变换，方 框内为元部件或系统的传递函数。

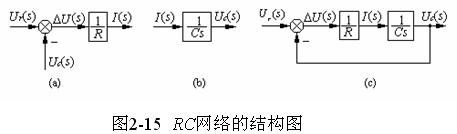
结构图：根据微分方程组得到的拉氏变换方程组，对每个子方程都用上述符号表示，并将各图形正确地连接起来，即为结构图，又称为方框图。

结构图也是系统的一种数学模型，它实际上是数学模型的图解化 。

（二）系统结构图的建立

建立系统的结构图，其步骤如下：

（1）建立控制系统各元部件的微分方程。

（2）对各元件的微分方程进行拉氏变换，并作出各元件的结构图。

（3）按系统中各变量的传递顺序，依次将各元件的结构图连接起来，置系统的输入变量于左端，输出变量于右端，便得到系统的结构图。

例2.1 试绘制图2-20所示无源网络的结构图。

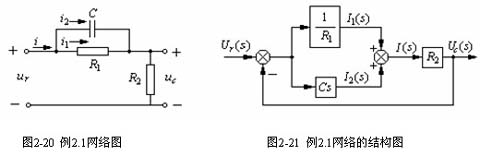
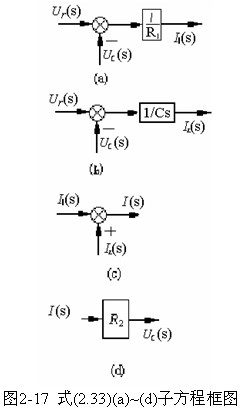
解 系统各部分微分方程经拉氏变换后的关系式为式(2.33)然后作出每个子方程的结构图，如图2-17(a)～(h)所示:

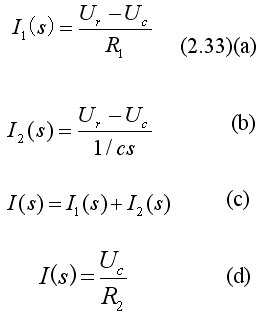
按系统中各元件的相互关系（确定各输入量和输出量）

将各方框连接起来（图2-21）。

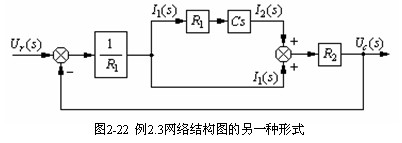
一个系统的结构图不是唯一的，但经过变换求得的总传递函数都应该是相同的。上例所示网络的结构图还可用图2-22表示。

（三）结构图的等效变换

结构图的运算和变换，就是将结构图化为一个等效的方框，使方框中的数学表达式为等效传递函数。

结构图的变换应按等效原理进行。

1．结构图的基本组成形式

（1）串联连接：方框与方框首尾相连。前一个方框的 输出，作为后一个方框的输入。
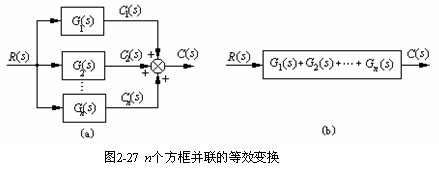
（2）并联连接：两个或多个方框，输入相同，输出为各方框输出的代数和。
（3）反馈连接：一个方框的输出，输入到另一个方框，得到的输出再返回作用于前一个方框的输入端。如图2-37所示。

图中A处为相加点，返回至A处的信号取“+”，称为正反馈；取“-”，称为负反馈。负反馈连接是控制系统的基本结构形式。

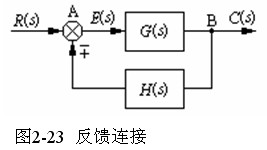
结构图中点B（位置）常称为引出点。

2．结构图的等效变换法则

（1）串联方框的等效变换

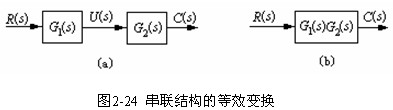
由图2-24可写出：

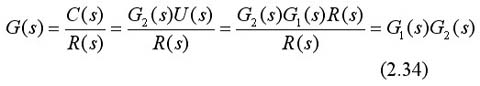
两个串联方框的等效传递函数等于该两个方框的传递函数的乘积。

n个环节并联，其等效传递函数为n个环节的传递函数的代数和，如图2-27所示：