一. 参数根轨迹
前面介绍的普通根轨迹或一般根轨迹的绘制规则是以开环根轨迹增益 为可变参数的,大多数系统都属于这种情况。但有时候,为了分析系统方便起见,或着重研究某个系统参数(如时间节数、反馈系数等)对系统性能的影响,也常常以这些参数作为可变参数绘制根轨迹,我们把以非开环根轨增益
作为可变参数绘制的根轨迹叫做参数根轨迹(或广义根轨迹)。下面先看—个例子。
例6-10 已知系统的开环传递函数为�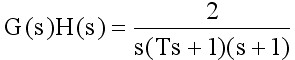
试绘制以时间常数 T 为可变参数的根轨迹。
解 ⑴系统的特征方程是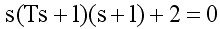
或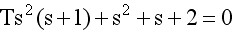
用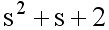 去除等式两边得 去除等式两边得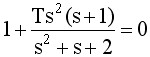
令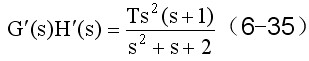
则有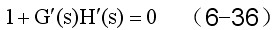
我们称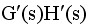 为系统的等效开环传递函数。在等效开环传递函数中,除时间常数T取代了普通根轨迹中开环根轨迹增益Kr的位置外,其形式与绘制普通根轨迹的开环传递函数完全一致,这样便可根据绘制普通根轨迹的七条基本规则来绘制参数根轨迹。 为系统的等效开环传递函数。在等效开环传递函数中,除时间常数T取代了普通根轨迹中开环根轨迹增益Kr的位置外,其形式与绘制普通根轨迹的开环传递函数完全一致,这样便可根据绘制普通根轨迹的七条基本规则来绘制参数根轨迹。
⑵系统特征方程的最高阶次是3,由规则一和规则二知,该系统有三条连续且对称于实轴的根轨迹,根轨迹的终点(T=∞)是等效开环传递函数的三个零点,即z1=z2=0,
z3=-1 ;本例中,系统的等效开环传递函数的零点数m=3,极点数n=2,即m>n。我们在前面已经指出,这种情况在实际物理系统中一般不会出现,然而在绘制参数根轨迹时,其等效开环传递函数却常常出现这种情况。
与n>m情况类似,这时我们认为有m-n条根轨迹起始于S平面的无穷远处(无限极点)。因此,本例的三条根轨迹的起点(T=0)分别为P1=-0.5±j0.866,P2=0.5-j0.866
和无穷远处(无限极点)。
由规则三知,实轴上的根轨迹是实轴上-1至-∞线段。
由规则六可求出两个等效开环复数极点的起始角分别为

由规则七可求出根轨迹与虚轴的两个交点,用s=jω代入特征方程得

由此得到虚部方程和实部方程分别为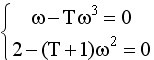
解虚部方程得ω的合理值为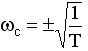 , ,
代入实部方程求得Tc=1秒,所以ωc=±1为根轨迹与虚轴的两个交点。
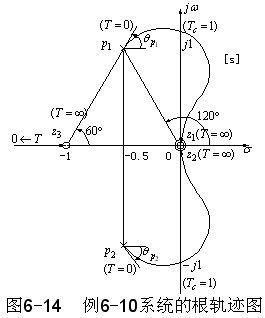
最后绘制出以时间常数T为可变参数的根轨迹图如图6-14所示。由根轨迹图可知,时间常数T=Tc=1 秒时,系统处于临界稳定状态,T>1秒时,根轨迹在S平面右半部,系统不稳定。由此可知,参数根轨迹在研究非开环根轨迹增益Kr对系统性能的影响是很方便的。
由上面的例子,可将绘制参数根轨迹的方法归纳为下述两个步骤:
⑴先根据系统的特征方程1+G(s)H(s)=0
求出系统的等效开环传递函数 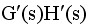 ,使 ,使
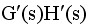 与绘制普通根轨迹的开环传递函数有相同的形式,即 与绘制普通根轨迹的开环传递函数有相同的形式,即
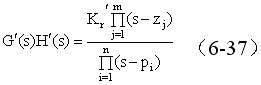
其中Kr'为除开环根轨迹增益Kr以外的任何参数,它是绘制参数根轨迹的可变参数。
⑵然后根据绘制普通根轨迹的七条基本规则和等效开环传递函数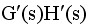 绘制出系统的参数根轨迹。 绘制出系统的参数根轨迹。
|

