一、绘制根轨迹的依据
根轨法的基本任务在于,由已知的开环零、极点的分布及根轨迹增益,通过图解的方法找出闭环极点。 由零变到无穷大时,闭环系统特征方程的根在S平面上运动的轨迹。因此,系统的特征方程便是绘制根轨迹的依据。系统的特征方程为
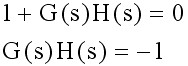
当系统有m个开环零点和n个开环极点时,特征方程可写成
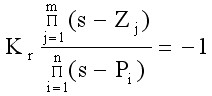
式中,Zj为已知的开环零点,Pi为已知的开环极点,Kr为可从零变到无穷的开环根轨迹增益。我们把上式称为根轨迹方程,由根轨迹方程,可以画出当Kr由零变到无穷时系统的根轨迹。
在绘制根轨迹时,参数不限定是根轨迹增益Kr,可为系统的其它参数(如时间常数、反馈系数等)这时只要把系统的特征方程化为上式,将感兴趣的参数取代根轨迹增益Kr的位置就可以绘制根轨迹。
根轨迹方程实际上是一个向量方程,用模和相角的形式表示就是
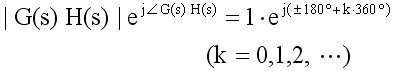
可得到满足系统特征方程的幅值条件和相值条件为
幅值条件: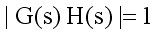
相值条件: 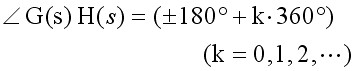
设系统的开环传递函数为
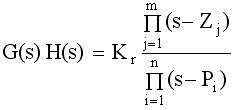
满足幅值条件的表达式为
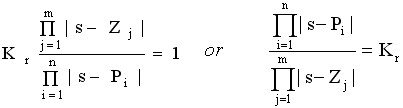
满足相角条件的表达式为
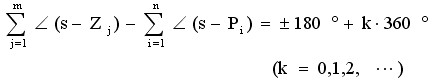
综上分析,可以得到如下结论:
⑴绘制根轨迹的相角条件与系统开环根轨迹增益 值的大小无关。即在S平面上,所有满足相角条件的点的集合的构成系统的根轨迹图。即相角条件是绘制根轨迹的主要依据。
⑵绘制根轨迹的幅值条件与系统开环根轨迹增益Kr值的大小有关。即Kr值的变化会改变系统的闭环极点在S平面上的位置。
⑶在系统参数确定的情况下,凡能满足相角条件和幅值条件的S值,就是对应给定参数的特征根,或系统的闭环极点。
⑷由于相角条件和幅值条件只与系统的开环传递函数有关,因此,已知系统的开环传递函数便可绘制出根轨迹图。
二、绘制根轨迹的基本规则
通常,我们把以开环根轨迹增益 为可变参数绘制的根轨迹叫做普通根轨迹(或一般根轨迹)。绘制普通根轨迹的基本规则如下。
规则一 根轨迹的起点和终点
幅值条件可写成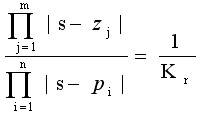
当Kr=0,必须有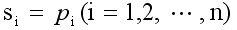 ,此时,系统的闭环极点与开环极点相同(重合),我们把开环极点称为根轨迹的起点,它对应于开环根轨迹增益Kr=0
。 ,此时,系统的闭环极点与开环极点相同(重合),我们把开环极点称为根轨迹的起点,它对应于开环根轨迹增益Kr=0
。
当Kr=∞时,必须有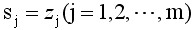 ,此时,系统的闭环极点与开环零点相同(重合),我们把开环零点称为根轨迹的终点,它对应于开环根轨迹增益Kr=∞。
,此时,系统的闭环极点与开环零点相同(重合),我们把开环零点称为根轨迹的终点,它对应于开环根轨迹增益Kr=∞。
下面分三种情况讨沦。
1.当m=n时,即开环零点数与极点数相同时,根轨迹的起点与终点均有确定的值。
2.当m<n时,即开环零点数小于开环极点数时,除有m条根轨迹终止于开环零点(称为有限零点)外,还有n-m条根轨迹终止于无穷远点(称为无限零点)。如例6-1。
3.当m>n时,即开环零点数大于开环极点数时,除有n条根轨迹起始于开环极点(称为有限极点)外,还有m-n条根轨迹起始于无穷远点(称为无限极点)。这种情况在实际的物理系统中虽不会出现,但在参数根轨迹中,有可能出现在等效开环传递函数中。
结论:根轨迹起始于开环极点Kr=0,终止于开环零点(Kr=∞或Kr→∞);如果开环极点数n大于开环零点数m,则有n-m条根轨迹终止于S平面的无穷远处(无限零点),如果开环零点数m大于开环极点数n,则有m-n条根轨迹起始于S平面的无穷远处(无限极点)。
规则二 根轨迹的分支数、连续性和对称性
根轨迹的分支数即根轨迹的条数。既然根轨迹是描述闭环系统特征方程的根(即闭环极点)在S平面上的分布,那么,根轨迹的分支数就应等于系统特征方程的阶数。
由例4-1看出,系统开环根轨迹增益Kr(实变量)与复变量S有一一对应的关系,当Kr由零到无穷大连续变化时,描述系统特征方程根的复变量S在平面上的变化也是连续的,因此,根轨迹是n条连续的曲线。
由于实际的物理系统的参数都是实数,如果特征方程有复数根,一定是对称于实轴的共轭复根,因此,根轨迹总是对称于实轴的。
结论:根轨迹的分支数等于系统的闭环极点数。根轨迹是连续且对称于实轴的曲线。
规则三 实轴上的根轨迹
若实轴上某线段右侧的开环零、极点的个数之和为奇数,则该线段是实轴上的根轨迹。
例4-3 设系统的开环传递函数为�
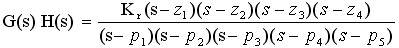
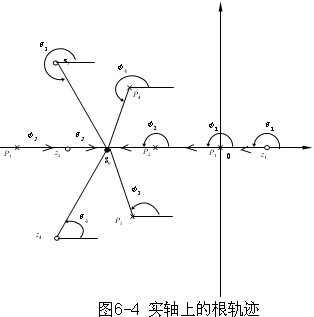
其中P1 、P2 、P3 、Z1 、Z2 为实极点和实零点,P4、P5、Z4、Z5 为共轭复数零、极点,它们在S平面上的分布如图4-4所示,试分析实轴上的根轨迹与开环零点和极点的关系。�
实轴上的根轨迹必须满足绘制根轨迹的相角条件,即�
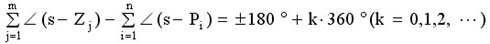
为确定实轴上的根轨迹,选择s0作为试验点。图6-4中,开环极点到s0点的向量的相角为
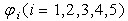 开环零点到s0点的向量的相角为 开环零点到s0点的向量的相角为
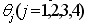
 确定实轴上的某点是否在根轨迹上时,可以不考虑复数开环零、极点对相角的影响。 确定实轴上的某点是否在根轨迹上时,可以不考虑复数开环零、极点对相角的影响。
实轴上,s0点左侧的开环极点P3和开环零点z2构成的向量的夹角均为零度,而s0点右侧的开环极点P1 、P2和开环零点z1构成的向量的夹角均为π。若s0为根轨迹上的点,必满足相角条件,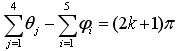
由以上分析知,只有s0点右侧实轴上的开环极点和开环零点的个数之和为奇数时,才满足相角条件。
|

