第三章已经介绍,闭环控制系统的稳定性由系统特征方程根的性质唯一确定。对于三阶以下系统,解出特征根就能判断系统是否稳定。三阶以上的高阶系统,求解特征根通常都很困难,前面介绍了两种判别系统稳定性的方法,基于特征方程的根与系数关系的劳斯判据和根轨迹法。
奈奎斯特(Nyquist)稳定判据(简称奈氏判据)是判断系统稳定性的又一重要方法。它是将系统的开环频率特性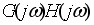 与复函数 与复函数
 位于S平面右半部的零、极点数目联系起来的一种判据。奈氏判据是根据系统的开环频率特性判断系统稳定性的一种图解法。由于系统的开环特性可用解析法或实验法获得,因此,应用奈氏判据分析系统的稳定性即方便又实用。奈氏判据还有助于建立相对稳定性的概念。 位于S平面右半部的零、极点数目联系起来的一种判据。奈氏判据是根据系统的开环频率特性判断系统稳定性的一种图解法。由于系统的开环特性可用解析法或实验法获得,因此,应用奈氏判据分析系统的稳定性即方便又实用。奈氏判据还有助于建立相对稳定性的概念。
一、幅角定理
幅角定理又称映射定理,它是建立在复变函数理论基础上的。简要地介绍幅角定理:设有一复变函数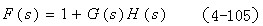 称之为辅助函数,其中G(s)H(s) 是系统的开环传递函数.
称之为辅助函数,其中G(s)H(s) 是系统的开环传递函数.
通常可写成如下形式
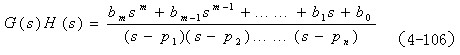
式中Pj(j=0,1,2,……) 是系统的开环极点,将式(4-106)代入式(4-105)得
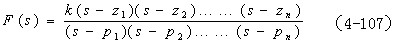
比较式(4—107)和式(4—106)可知,辅助函数F(s) 的零点Zi(i=0,1,2,……) 等于系统闭环传递函数的极点,即系统特征方程1+G(s)H(s)=0
的根。因此,如果辅助函数F(s) 的零点都具有负的实部,即都位于S平面的左半部,系统就是稳定的,否则系统便不稳定。
一)S平面与F(s) 平面的映射关系
假设复变函数F(s) 为单值函数,且除了S平面上有限的奇点外,处处都为连续的正则函数,也就是说F(s) 在S平面上除奇点外处处解析,
那么,对于S平面上的每个解析点,在F(s) 平面上必有一点(称为映射点)与之对应。
例如,当系统的开环传递函数为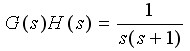
则其辅助函数是 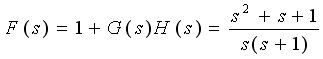
除奇点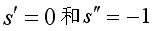 外,在S平面上任取一点,如
外,在S平面上任取一点,如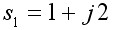
则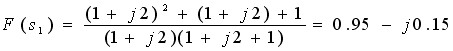
如图4-37所示,在F(s)平面上有点F(s)=0.95-j0.15 与S平面上的点S1 对应,F(s1)就叫做s1=1+j2
在F(s)平面上的映射点。
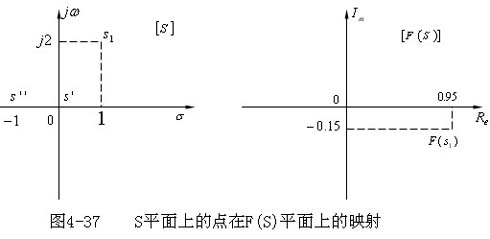
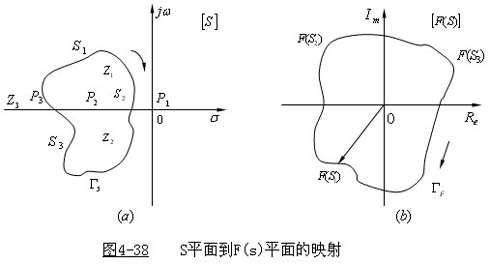
如图4-38所示,如果解析点S1 在S平面上沿封闭曲线Γs ,(Γs 不经过F(s)的奇点)按顺时针方向连续变化一周,那么辅助函数F(s)在
F(s)平面上的映射也是一条封闭曲线Γf,但其变化方向可以是顺时针的,也可以是逆时针的,这依据辅助函数F(s) 的性质而定。
(二)幅角定理(映射定理)
设F(s) 在S平面上,除有限个奇点外,为单值的连续正则函数,若在S平面上任选一封闭曲线Γs,并使Γs不通过 的奇点,则S平面上的封闭曲线Γs
映射到F(s)平面上也是一条封闭曲线ΓF。当解析点s按顺时针方向沿Γs 变化一周时,则在 平面上, ΓF 曲线按逆时针方向旋转的周数N(每旋转2?弧度为一周),或
ΓF 按逆时针方向包围 F(s)平面原点的次数,等于封闭曲线?s内包含F(s) 的极点数P与零点数Z之差。即 N=P-Z
(5-108),式中,若N>0,则ΓF按逆时针方向绕F(s)平面坐标原点N周;若N<0,则ΓF按顺时针绕
F(s)平面坐标原点N周;且若 N=0,则?F不包围F(s)平面坐标原点。
在图4-38中,在S平面上有三个极点P1、P2 、P3和三个零点Z1、Z2、Z3 。被Γs 曲线包围的零点有Z1、Z2两个,即Z=2,包围的极点只有P2
,即P=1,由式(4-108)得
N=P-Z=1-2=-1
说明Γs 映射到 F(s)平面上的封闭曲线ΓF顺时针绕F(s)平面原点一周。
由幅角定理,我们可以确定辅助函数 被封闭曲线Γs 所包围的极点数P与零点数 Z的差值P-Z。
前面我们已经指出, 的极点数等于开环传递函数 的极点数,因此当我们从 平面上确定了封闭曲线ΓF 的旋转周数N以后,则在
S 平面上封闭曲线Γs 包含的零点数Z(即系统的闭环极点数)便可简单地由下式计算出来Z=P-N (4-109)
封闭曲线Γs和ΓF 的形状是无关紧要的,它不影响上述结论。
关于幅角定理的数学证明请读者参考有关书籍,这里仅从几何图形上简单说明。
设有辅助函数为
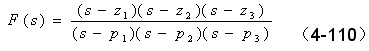
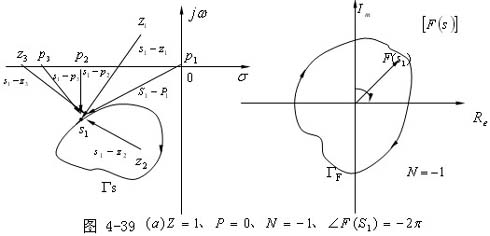
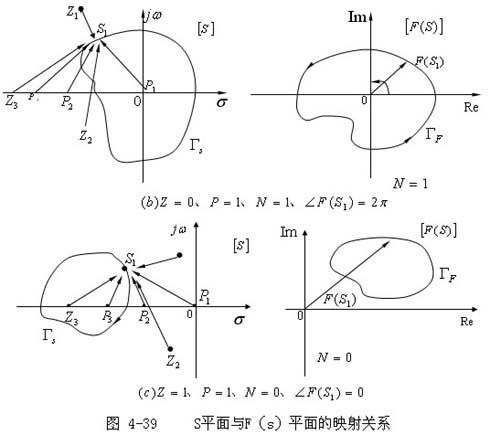
其零、极点在S平面上的分布如图 4—39 所示,在 S平面上作一封闭曲线Γs , Γs不通过上述零、极点,在封闭曲线Γs
上任取一点F(s1) , 其对应的辅助函数的幅角应为
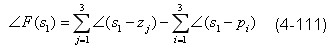
当解析点S1沿封闭曲线Γs按顺时针方向旋转一周后再回到 s1 点,从图中可以发现,所有位于封闭曲线Γs 外面的辅助函数的零、极点指向s1
的向量转过的角度都为0,而位于封闭曲线Γs 内的辅助函数的零、极点指向s1 的向量都按顺时针方向转过2弧度(一周)。这样,对图4—39(a),Z=1,P=0,
,即 N=-1,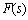 绕F(s1)平面原点顺时针旋转一周;对图4—39(b),Z=0,P=1,
绕F(s1)平面原点顺时针旋转一周;对图4—39(b),Z=0,P=1,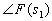 =-2π
,即N=1, =-2π
,即N=1,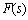 绕F(s1)平面原点逆时针旋转一周;对图4—39(c),Z=1,P=1,
绕F(s1)平面原点逆时针旋转一周;对图4—39(c),Z=1,P=1,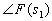 =2π
,即N=0, =2π
,即N=0,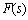 不包围F(s1)
平面原点。将上述分析推广到一般情况则有 不包围F(s1)
平面原点。将上述分析推广到一般情况则有
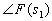 =2π(P-Z)=2πN
(4-112) =2π(P-Z)=2πN
(4-112)
由此得到幅角定理表达式为 N=P-Z (4-113)
二、基于辅助函数F(s)的奈氏判据
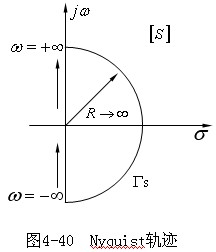 为了分析反馈控制系统的稳定性,只须判断是否存在S平面右半部的闭环极点。为此,在S平面上作一条完整的封闭曲线Γs,使它包围S平面右半部且按顺时针环绕。如图5—40所示,该曲线包括S平面的整个虚轴(由ω=-∞到ω=+∞)及右半平面上以原点为圆心,半径为无穷大的半圆弧组成的封闭轨迹。这一封闭无穷大半圆称作奈氏轨迹。显然,由奈氏轨迹包围的极点数P和零点数Z,就是F(s)位于S平面右半部的极点数和零点数。 为了分析反馈控制系统的稳定性,只须判断是否存在S平面右半部的闭环极点。为此,在S平面上作一条完整的封闭曲线Γs,使它包围S平面右半部且按顺时针环绕。如图5—40所示,该曲线包括S平面的整个虚轴(由ω=-∞到ω=+∞)及右半平面上以原点为圆心,半径为无穷大的半圆弧组成的封闭轨迹。这一封闭无穷大半圆称作奈氏轨迹。显然,由奈氏轨迹包围的极点数P和零点数Z,就是F(s)位于S平面右半部的极点数和零点数。
前面已经指出,辅助函数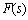 的极点等于系统的开环极点,
的极点等于系统的开环极点,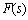 的零点等于系统的闭环极点。因此,如果奈氏轨迹中包围 的零点等于系统的闭环极点。因此,如果奈氏轨迹中包围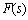 的零点数Z=0,系统是稳定的,此时由 的零点数Z=0,系统是稳定的,此时由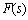 映射到 映射到
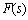 平面上的封闭曲线ΓF
逆时针绕 平面坐标原点的周数应为 N=P (4-114) 平面上的封闭曲线ΓF
逆时针绕 平面坐标原点的周数应为 N=P (4-114)
由此得到应用幅角定理分析系统稳定性的判据如下:
若辅助函数 的解析点S沿奈氏轨迹Γs 按顺时针连续环绕一周,它在
平面上的映射ΓF 按逆时针方向环绕其原点 P周,则系统是稳定的,否则是不稳定的。
通常情况下,开环系统是稳定的,即S平面右半部的开环极点数P=0。此时系统稳定的充分条件是不包围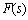 平面坐标原点,即 N=0。
平面坐标原点,即 N=0。
|

