5.4.1 Z变换
由式(5-5)可知,x*(t)的拉氏变换为
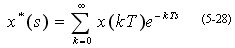
若令 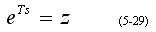
则S域分析的问题变成Z域的分析问题。
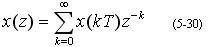
x(z)称为x*(t)的z 变换,记为 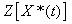
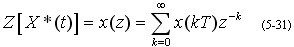
在Z变换中, x(z) 为采样脉冲序列的Z变换,即只考虑采样时刻的信号值。由于在采样时刻,x(z)的值就是x(kT),所以从这个意义上说,
x(z) 既是x*(t)的Z变换,也可以写为x(t)的Z变换,即
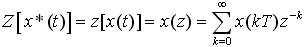 (5-32)
(5-32)
例:已知函数 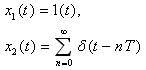 ,求它们的Z变换。 ,求它们的Z变换。
解: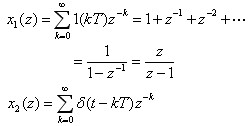
5.4.2 Z变换的性质�
(1)线性定理
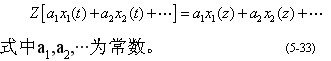
(2) 实平移定理
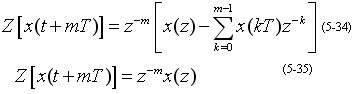
(3)复平移定理
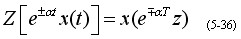
例 已知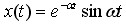 , 求x(z)
, 求x(z)
解 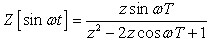
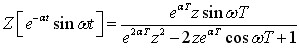
(4)复域微分定理
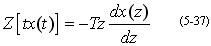
例 已知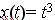 ,求 x(z)
,求 x(z)
解 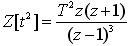
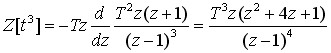
(5)初值定理
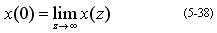
证明:由Z变换的定义有
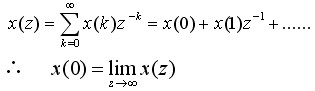
(6) 终值定理
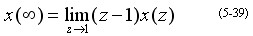
证明 : 由Z变换的定义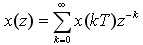
由实位移定理
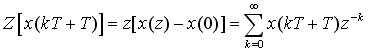
上二式相减有
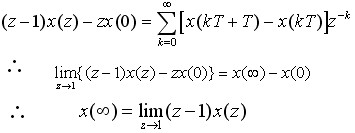
例 已知 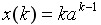 求的z变换 求的z变换
解 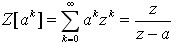
由实位移定理有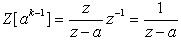
由微分定理有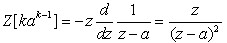
5.4.3 Z反变换
(1)幂级数法
通常Z变换表达式为如下形式:

用综合除法有 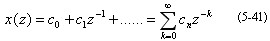
由Z变换的定义式可知 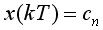
则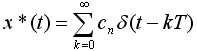 即为x(z)的原函数
即为x(z)的原函数
例 求 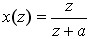 原函数的解 原函数的解
解 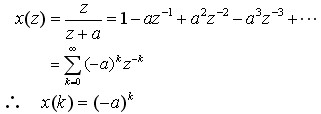
(2)部分分式法
部分分式法又称查表法。基本思想是将x(z)/z展开成部分分式,
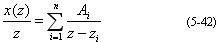
然后,查z变换表,即可求取x(z)的原函数x(kT)
例 已知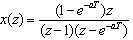 求 x(kT)
求 x(kT)
解: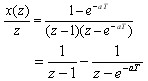
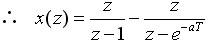
查Z变换表有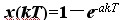
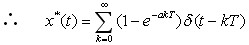
|

