5.6.1 线性离散控制系统的稳定性分析
线性离散控制系统的闭环脉冲传递函数,如图5-30所示,
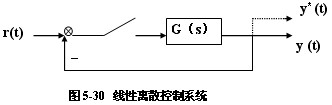
可求得为: 
则线性离散控制系统的特征方程为 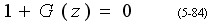
考察下式 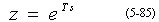
假定在s平面上任有一点 
则通过Z变换,映射到Z平面为 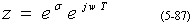
当δ=0,即s平面的虚轴,对应Z平面的单位圆。
当δ<0,即左半s平面对应Z平 面的单位圆内。Z平面单位圆内为稳定区域。 面的单位圆内。Z平面单位圆内为稳定区域。
当δ>0,即右半s平面对应Z平面的单位圆外部区域,Z平面单位圆外的部分为不稳定域。上面映射关系如图5-31所示。
线性离散控制系统稳定的充分必要条件是:线性离散闭环控制系统特征方程根的模小于1,则线性离散控制系统是稳定的。
例 已知离散控制系统结构如图所示,采样周期T=1秒,分析系统的稳定性。
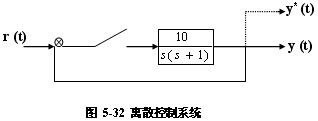
解: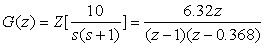
闭环特征方程 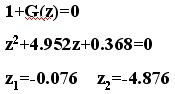
系统特征方程的根有一个在单位圆外,因此,该离散系统不稳定。
在离散系统中,引进双线性变换。
令 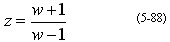
或 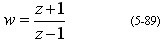
其中Z和W可写为 
将式(5-90)代入式(5-89),有
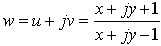
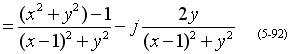
 于是,当 于是,当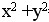 =1
, 即对应Z平面上的单位圆即u=0,为W平面上的虚轴 =1
, 即对应Z平面上的单位圆即u=0,为W平面上的虚轴
当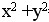 <1,
即Z平面上单位圆内的部分,也即稳定域u<0为左半W平面左半平面(稳定域) <1,
即Z平面上单位圆内的部分,也即稳定域u<0为左半W平面左半平面(稳定域)
当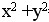 >1
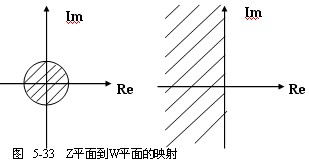
即Z平面上单位圆内外的部分,也即不稳定域u>0, 即右半W平面对应不稳定域。上面映射关系如图5-33所示。 >1
即Z平面上单位圆内外的部分,也即不稳定域u>0, 即右半W平面对应不稳定域。上面映射关系如图5-33所示。
|

