三、基于开环传递函数 的奈氏判据
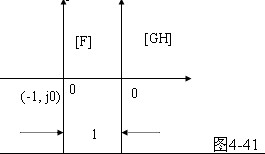 用辅助函数 用辅助函数 来分析系统的稳定性仍然不大方便, 实际上, 开环传递函数与辅助函数之间的关系非常简单,即
来分析系统的稳定性仍然不大方便, 实际上, 开环传递函数与辅助函数之间的关系非常简单,即
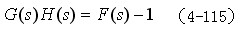
上式意味着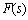 平面的纵轴向右平移一个单位后构成的平面即为
GH平面(如图4-41)。 平面的纵轴向右平移一个单位后构成的平面即为
GH平面(如图4-41)。
F(s)平面的坐标原点是GH 平面的(-1,j0)点。因此,ΓF 绕 平面原点的周数等效于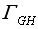 绕GH平面(-1,j0)
点的周数。 绕GH平面(-1,j0)
点的周数。
由上面的分析,得到基于开环传递函数G(s)H(s)的奈氏判据如下:
闭环系统稳定的充分必要条件是奈氏轨迹映射在GH平面上的封闭曲线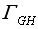 逆时针包围
(-1,j0)点P周,其中P为开环传递函数G(s)H(s)在S平面右半部的极点数。 逆时针包围
(-1,j0)点P周,其中P为开环传递函数G(s)H(s)在S平面右半部的极点数。
当G(s)H(s)在S平面右半部没有极点时,即P=0,闭环系统稳定的充分必要条件是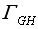 在GH平面上不包围(-1,j0)点。 在GH平面上不包围(-1,j0)点。
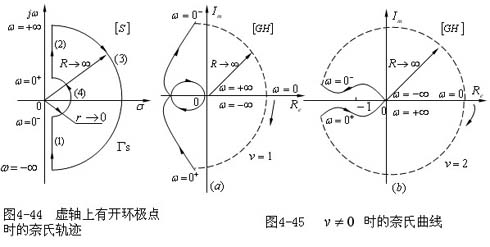
当G(s)H(s)在S平面的虚轴上(包括原点)有极点时,由于奈氏轨迹不能经过开环极点,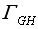 必须避开虚轴上的所有开环极点。图4-44表示当有开环极点为零时的奈氏轨迹,其中(1)(2)
和(3)部分的定义与图4—42相同. 必须避开虚轴上的所有开环极点。图4-44表示当有开环极点为零时的奈氏轨迹,其中(1)(2)
和(3)部分的定义与图4—42相同.
第(4)部分的定义是: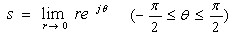
表明S沿以原点为圆心,半径为无穷小的右半圆弧上逆时针变化(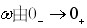 )。这样,
Γs 即绕过了G(s)H(s)原点上的极点, 又包围了整个右半S平面,如果在虚轴上还有其它极点,亦可采用同样的方法,将Γs
绕过这些虚轴上的极点。 )。这样,
Γs 即绕过了G(s)H(s)原点上的极点, 又包围了整个右半S平面,如果在虚轴上还有其它极点,亦可采用同样的方法,将Γs
绕过这些虚轴上的极点。
设系统的开环传递函数为
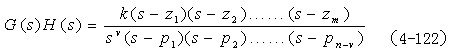
其中v为系统中积分环节的个数。当 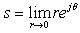 时, 时,
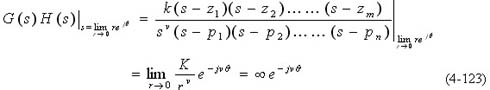
式(4-123)表明,Γs 的第(4)部分无穷小半圆弧在 GH平面上的映射为顺时针旋转的无穷大圆弧,旋转的弧度为vπ弧度。图4—45(a)、(b)分别表示当
v=1和v=2时系统的奈氏曲线,其中虚线部分是?s 的无穷小半圆弧在GH平面上的映射。
基于开环频率特性的奈氏判据如下:
奈奎斯特稳定判据:
闭环系统稳定的充分必要条件是,GH 平面上的开环频率特性 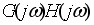 当ω由-∞变化到+∞时,奈氏曲线按逆时针方向包围(-1,j0)点P周。 当ω由-∞变化到+∞时,奈氏曲线按逆时针方向包围(-1,j0)点P周。
当位于S平面右半部的开环极点数P=0时,即当系统的开环传递函数的全部极点均位于S平面左半部(包括原点和虚轴)时,闭环系统稳定的充分必要条件是奈氏曲线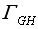 不包围GH平面的(-1,j0)点。 不包围GH平面的(-1,j0)点。
综上所述,应用奈氏判据分析系统稳定性时,可能会遇到下列三种情况:
(i) 当系统开环传递函数G(s)H(s)的全部极点都位于S平面左半部时(P=0),如果系统的奈氏曲线 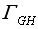 不包围GH平面的(-1,j0)点(N=0),则闭环系统是稳定的(z=p-N=0),否则是不稳定的; 不包围GH平面的(-1,j0)点(N=0),则闭环系统是稳定的(z=p-N=0),否则是不稳定的;
(ii) 当系统开环传递函数G(s)H(s)有p个位于S平面右半部的极点时,如果系统的奈氏曲线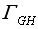 逆时针包围(-1,j0)点的周数等于位于S平面右半部的开环极点数
(N=P),则闭环系统是稳定的(Z=P-N=0),否则是不稳定的; 逆时针包围(-1,j0)点的周数等于位于S平面右半部的开环极点数
(N=P),则闭环系统是稳定的(Z=P-N=0),否则是不稳定的;
(iii) 如果系统的奈氏曲线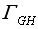 顺时针包围点(-1,j0)(N>0),则闭环系统不稳定。
(Z=P-N>0)。 顺时针包围点(-1,j0)(N>0),则闭环系统不稳定。
(Z=P-N>0)。
从上面的分析可知,奈氏曲线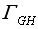 是否包围GH平面的(-1,j0)点是判别系统是否稳定的重要依据(当然还须考虑是否存S平面右半部的开环极点和 是否包围GH平面的(-1,j0)点是判别系统是否稳定的重要依据(当然还须考虑是否存S平面右半部的开环极点和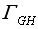 曲线包围(-1,j0)点的方向)。在有些情况下, 曲线包围(-1,j0)点的方向)。在有些情况下,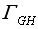 曲线恰好通过GH平面的(-1,j0)点(注意不是包围),此时如果系统无位于S平面右半部的开环极点,则系统处于临界稳定状态。 曲线恰好通过GH平面的(-1,j0)点(注意不是包围),此时如果系统无位于S平面右半部的开环极点,则系统处于临界稳定状态。
五、奈氏判据的应用
例4—6 试用奈氏判据分析例4—1系统的稳定性。
解 该系统的开环传递函数为
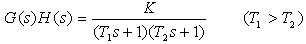
其对应的频率特性是
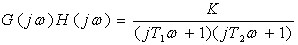
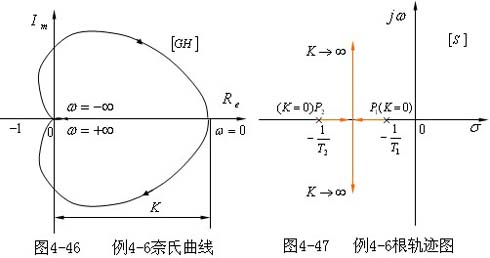
开环频率特性的极坐标图如图 4—24所示,当ω:-∞~+∞ 时系统的奈氏曲线如 图4—46所示。由该系统的两个开环极点 均在S平面左半部,即S平面右半部的开环极点数P=0,由图4—46可知,系统的奈氏曲线 均在S平面左半部,即S平面右半部的开环极点数P=0,由图4—46可知,系统的奈氏曲线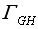 不包围(-1,j0)点(N=0),根据奈氏判据,位于S平面右半部的闭环极点数
Z=P-N=0, 该闭环系统是稳定的。 不包围(-1,j0)点(N=0),根据奈氏判据,位于S平面右半部的闭环极点数
Z=P-N=0, 该闭环系统是稳定的。
上述结论可从图 4—47所示的根轨图得到证明,从图4—47可知,无论K为何值根轨迹都在S平面左半部,系统总是稳定的。
例4—7 试用奈氏判据分析例4-3系统的稳定性。
解 该系统的开环传递函数为
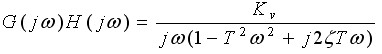
其对应的频率特性是
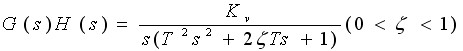
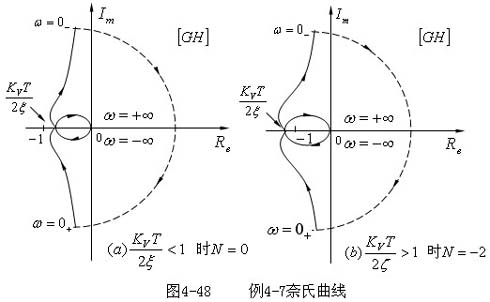
开环频率特性的极坐标图如图4—48所示,当ω:-∞~+∞时,
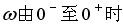 系统的奈氏曲线如图
4-48所示。由于系统含有一个积分环节(v=1),当对应奈氏曲线为顺时针环绕坐标原点的无穷大半圆(图4-48中虚线所示)。 系统的奈氏曲线如图
4-48所示。由于系统含有一个积分环节(v=1),当对应奈氏曲线为顺时针环绕坐标原点的无穷大半圆(图4-48中虚线所示)。
开环传递函数无右半S平面的极点,即P=0,系统是否稳定取决于奈氏曲线与负实轴的交点坐标值-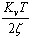 的大小,当
的大小,当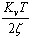 <
1 时, <
1 时,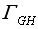 不包围(-1,j0)点,即N=0图4-48(a),系统是稳定的;当 不包围(-1,j0)点,即N=0图4-48(a),系统是稳定的;当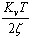 >
1 时,奈氏曲线 >
1 时,奈氏曲线 顺时针包围(-1,j0)点两周,即N=-2,图4—48(b),系统不稳定。 顺时针包围(-1,j0)点两周,即N=-2,图4—48(b),系统不稳定。
例4—8 已知反馈控制系统的开环传递函数为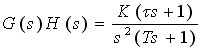
试用奈氏判据分析当 时系统的稳定性。
解 系统的开环频率特性是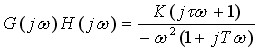
其幅频特性和相频特性分别是
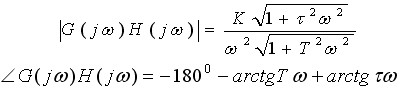
(a)当T<τ时, 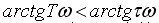 ,
当ω由0变至+∞时, 由∞变至0, ,
当ω由0变至+∞时, 由∞变至0, 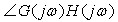 由-180度在第III象限内变化为-180度,其对应的奈氏曲线如图4-50(a)所示,图中虚线表示的顺时针旋转的无穷大圆弧是开环零重极点在
GH 平面上的映射。由于奈氏曲线左端无穷远处是开口的,它没有包围(-1,j0)点(N=0),系统无S平面右半部的开环极点(P=0),由奈氏判据知,当T<τ时,该系统是稳定的。 由-180度在第III象限内变化为-180度,其对应的奈氏曲线如图4-50(a)所示,图中虚线表示的顺时针旋转的无穷大圆弧是开环零重极点在
GH 平面上的映射。由于奈氏曲线左端无穷远处是开口的,它没有包围(-1,j0)点(N=0),系统无S平面右半部的开环极点(P=0),由奈氏判据知,当T<τ时,该系统是稳定的。
(b) 当T=τ时,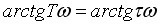 ,系统的相频特性
,系统的相频特性
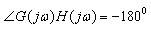 与角频率ω无关,幅频特性|G(jω)H(jω)|,当ω由0变至+∞时,由∞变至0
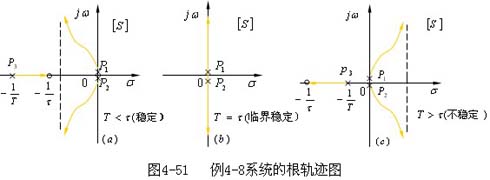
。如图4-50(b)所示,除无穷大圆弧外,奈氏曲线是穿过(-1,j0)点且与负实轴重合的,系统是临界稳定状态。当T=τ时,系统的根轨迹如图4-51(b)
所示。由于两条根轨迹位于S平面的虚轴上,系统是等幅振荡的临界稳定状态。 与角频率ω无关,幅频特性|G(jω)H(jω)|,当ω由0变至+∞时,由∞变至0
。如图4-50(b)所示,除无穷大圆弧外,奈氏曲线是穿过(-1,j0)点且与负实轴重合的,系统是临界稳定状态。当T=τ时,系统的根轨迹如图4-51(b)
所示。由于两条根轨迹位于S平面的虚轴上,系统是等幅振荡的临界稳定状态。
(c)当T>τ时, 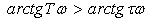 ,当ω由0变至+∞时,|G(jω)H(jω)|
由∞变至0, ,当ω由0变至+∞时,|G(jω)H(jω)|
由∞变至0, 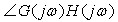 由-180度在第II象限内变化后再次变为-180度,其对应的奈氏曲线如图4-50(c)所示。由于奈氏曲线左端是封口的,它顺时针包围了
(-1,j0)点两周(N=2),由奈氏判据知,当T>τ时,该系统是不稳定的。当T>τ时,系统的根轨迹如图4—51(c)所示。由于有两条根轨迹全部位于S平面右半部,无论K为何值,该系统都是不稳定的。 由-180度在第II象限内变化后再次变为-180度,其对应的奈氏曲线如图4-50(c)所示。由于奈氏曲线左端是封口的,它顺时针包围了
(-1,j0)点两周(N=2),由奈氏判据知,当T>τ时,该系统是不稳定的。当T>τ时,系统的根轨迹如图4—51(c)所示。由于有两条根轨迹全部位于S平面右半部,无论K为何值,该系统都是不稳定的。
|

