规则四 渐近线
当开环极点数n大于开环零点数m时,系统有n-m条根轨迹终止于S平面的无穷远处,这n-m条根轨迹变化趋向的直线叫做根轨迹的渐近线,因此,浙近线也有n-m条,且它们交于实轴上的一点。渐近线与实轴的交点位置σa和与实轴正方向的交角φa分别为
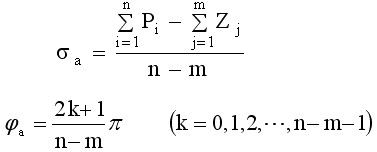
在例6-1中,开环传递函数为 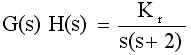
开环极点数n=2,开环零点数m=0,n-m=2,两条渐近线在实轴上的交点位置为
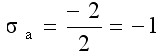 它们与实轴正方向的交角分别为π/2(k=0)和3π/2
,两条渐近线正好与Kr≥1时的根轨迹重合。 它们与实轴正方向的交角分别为π/2(k=0)和3π/2
,两条渐近线正好与Kr≥1时的根轨迹重合。
例6-2 已知系统的开环传递函数为�试画出该系统根轨迹的渐近线。
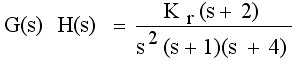
试画出该系统根轨迹的渐近线。
解 对于该系统有n=4,m=1,n-m=3;三条渐近线与实轴交点位置为
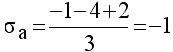
它们与实轴正方向的交角分别是
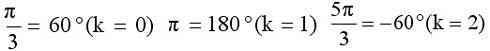
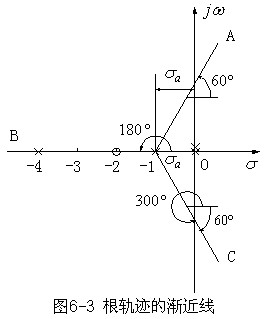
渐近线如图6-3所示。
规则五 根轨迹的分离点
分析例6-1,当系统开环增益 由零到无穷大变化时,两条根轨迹先是在实轴上相向运动( 0≤Kr<1),然后它们相遇在(-1,j0)点
,当 后,它们便离开实轴进入S平面,且离开实轴时,根轨迹与实轴正交。我们称该点为根轨迹的分离点。实际上,(-1,j0)点是例6-1系统特征方程的等实根,它对应的系统开环根轨迹增益Kr=1。一般,常见的根轨迹分离点是位于实轴上两条根轨迹分支的分离点。如例6-1中的(-1,j0)点。若根轨迹位于实轴上两个相邻的开环极点之间(其中一个可以是无限极点),则在这两个极点之间至少存在一个分离点;若根轨迹位于实轴上两个相邻的开环零点之间(其中一个可以是无限零点),则在这两个零点之间也至少有一个分离点。如图6-5上的分离点d1和d2。但在有些情况下,根轨迹的分离点也可能以共轭形式成对出现在复平面上,如图6-6中的分离点A和B。显然,复平面上的分离点表明系统特征方程的根中至少有两对相等的共轭复根存在。
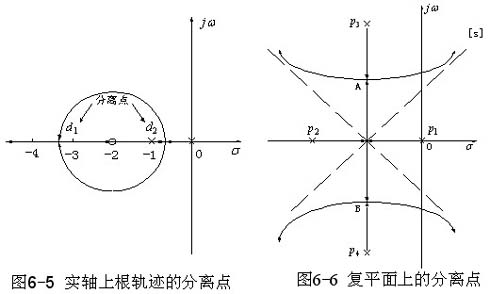
由上面分析可知,确定根轨迹的分离点,实质上就是求出系统特征方程的等实根(实轴上的分离点)或等共轭复根(复平面上的分离点)。
系统的特征方程可写成
对式(6-22)求导可得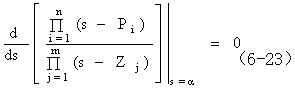
式(6-23)称为分离点方程。对于一个n阶系统,解式(6-23)可得到n-1个根
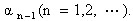
分离点方程的另一种形式为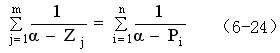
式中,Zj为开环零点的数值,Pi为开环极点的数值。
当开环系统无有限零点时,则在方程(6-24)中,应取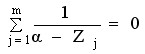
。此时,分离点方程即为 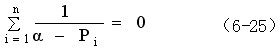
只有那些在根轨迹上的解才是根轨迹的分离点。若在这些根中有共轭复根,如何判断共轭复根是否在根轨迹上,是一个比较复杂的问题,但由于只有当开环零、极点分布非常对称时,才会出现复平面上的分离点(如图6-6所示),因此,用观察法可大体上判断,然后将其代入特征方程中进行验算,即可确定。
对于例6-1,由式(6-23)可得分离点方程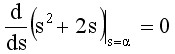
即 2α+2=0
解得α=-1,α=-1 位于实轴根轨迹上(由0到-2的线段上),故它是实轴上的分离点。
例6-4 已知系统的开环传递函数为�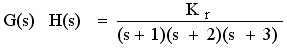
试求出系统根轨迹与实轴的交点。
 解
本系统无有限开环零点,由式(6-25) 解
本系统无有限开环零点,由式(6-25)
可得 
即 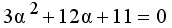
解出α1=-1.42,α2=-2.58,
由规则五知, 实轴上的根轨迹为 -1 到 -2 线段和-3到-∞线段。 不在上述两线段上,α2=-2.58应舍去。α1=-1.42是实轴根轨迹上的点,它就是根轨迹在实轴上的分离点。运用前面的六条规则,可绘制如图6-7所示的根轨迹图。
规则六 起始角与终止角
当开环传递函数中有复数极点或零点时,根轨迹是沿着什么方向离开开环复数极点或进入开环复数零点的呢?这就是所谓的起始角和终止角问题,
先给出定义如下:
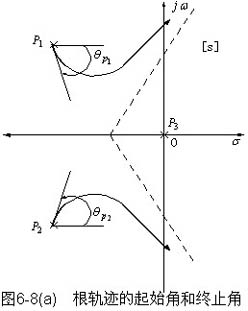
⑴起始角 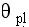 根轨迹离开开环复数极点处在切线方向与实轴正方向的夹角。参看图4-8(a)中的 根轨迹离开开环复数极点处在切线方向与实轴正方向的夹角。参看图4-8(a)中的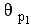 和 和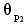 。 。
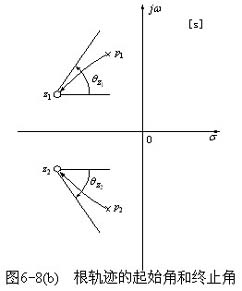
⑵终止角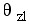 根轨迹进入开环复数零点处的切线方向与实轴正方向的夹角。参看图6-8(b)中的 根轨迹进入开环复数零点处的切线方向与实轴正方向的夹角。参看图6-8(b)中的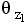 和 和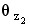 。 。
通过例6-5分析起始角与终止角的大小。
例6-5 已知系统的开环传递函数为
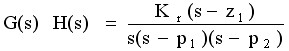 且P1和P2为一对共轭复数极点,P3和Z1分别为实极点和实零点,它们在S平面上的分布如图6-9所示。试依据相角条件求出根轨迹离开开环复数极点P1和P2的起始角 且P1和P2为一对共轭复数极点,P3和Z1分别为实极点和实零点,它们在S平面上的分布如图6-9所示。试依据相角条件求出根轨迹离开开环复数极点P1和P2的起始角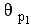 和 和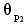 。
。
对于根轨迹上无限靠近p1的点A,由相角条件可得

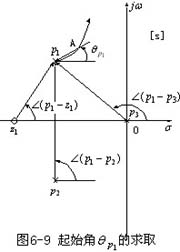 由于A点无限靠近P1点,
由于A点无限靠近P1点,
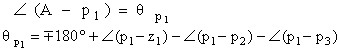
推广为一般情况可得求起始角的关系式为
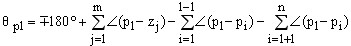
同理,可得到求终止角的关系式为
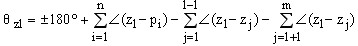
规则七 根轨迹与虚轴的交点
根轨迹与虚轴的交点就是闭环系统特征方程的纯虚根(实部为零)。这时,用s=jω 代入特征方程可得
即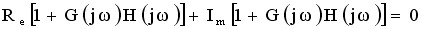
由此可得虚部方程和实部方程为
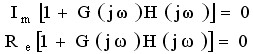
解虚部方程可得角频率ωc,即根轨迹与虚轴的交点的坐标值;用ωc代入实部方程,可求出系统开环根轨迹增益的临界值Krc
。Krc的物理含义是使系统由稳定(或不稳定)变为不稳定(或稳定)的系统开环根轨迹增益的临界值。
例6-6 试求出例6-4中根轨迹与虚轴的交点ωc及相应的开环根轨迹增益的临界值Krc。
解 由例6-4知系统的开环传递函数为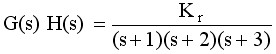
其特征方程是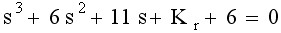
令s=jω并代入特征方程得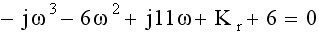
其虚部和实部方程分别为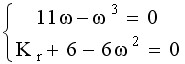
解虚部方程得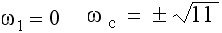
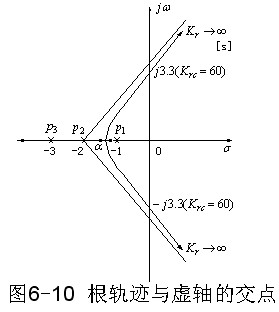
由于ω1=0不是根轨迹上的点,应舍去,故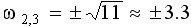 为根轨迹与虚轴的两个交点。将其代入实部方程便可求出系统开环根轨迹增益的临界值Krc=60。系统的根轨迹如图6-10所示。 为根轨迹与虚轴的两个交点。将其代入实部方程便可求出系统开环根轨迹增益的临界值Krc=60。系统的根轨迹如图6-10所示。
当系统的阶次较高时,解特征方程将会遇到困难,此时可用劳斯判据求出系统开环根轨迹增益的临界值Krc和根轨迹与虚轴的交点ωc。
以上七条规则是绘制根轨迹图所必须遵循的基本规则。此外,绘制一幅完整的根轨迹图尚须注意以下几点规范画法。
⑴根轨迹的起点(开环极点Pi)用符号“×”标示; 根轨迹的终点( 开环零点 ) 用符号“ 。”标示。
⑵根轨迹由起点到终点是随系统开环根轨迹增益Kr值的增加而运动的,要用箭头标示根轨迹运动的方向。
⑶要标出一些特殊点的Kr值,其中直接标出的有起点( Kr=0或Kr→0),终点 Kr=∞或Kr→∞);根轨迹与实轴的交点即实轴上的分离点
(Kr=Kra,α);与虚轴的交点(Kr=Kra,ωc)。还有一些要求标出的闭环极点S1及其对应的开环根轨迹增益K1,也应在根轨迹图上标出,以便于进行系统的分析和综合。
|

