二、劳斯判据
(一)系统稳定性的初步判别
已知系统的闭环特征方程为
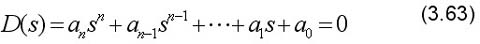
式中所有系数均为实数,且an>0,则系统稳定的必要条件是系统特征方程的所有系数均为正数。证明如下:
设式(3.63)有n个根,其中k个实根-pj(j=1,2,…,k),r对复根- s i ±jwi (i=1,2,…,r),n
= k+2r。则特征方程式可写为
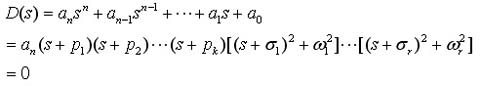
假如所有的根均在左半平面,即- pj <0,-σi<0 ,则pj >0 ,σi >0 。所以将各因子项相乘展开后,式(3.63)的所有系数都是正数。
根据这一原则,在判别系统的稳定性时,首先检查系统特征方程的系数是否都为正数,假如有任一系数为负数或等于零(缺项),则系统就是不稳定的。但是,假若特征方程的所有系数均为正数,并不能肯定系统是稳定的,还要做进一步的判别。因为上述所说的原则只是系统稳定性的必要条件,而不是充分必要条件。
(二) 劳斯判据
这是1877年由劳斯(Routh)提出的代数判据。
1. 若系统特征方程式
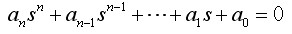
设an > 0,各项系数均为正数。
2. 按特征方程的系数列写劳斯阵列表:
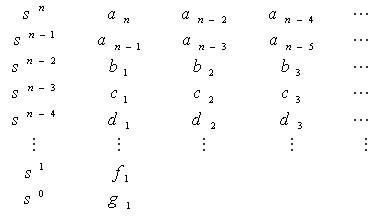
表中
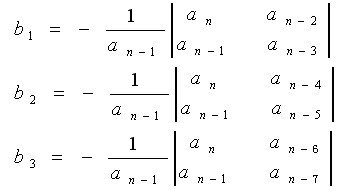 直至其余bi项均为零。
直至其余bi项均为零。
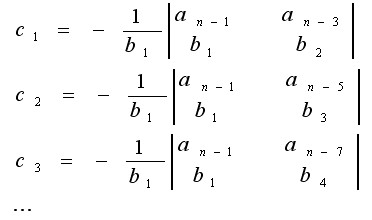
按此规律一直计算到n -1行为止。在计算过程中,为了简化数值运算,可将某一行中的各系数均乘一个正数,不会影响稳定性结论。
3. 考察阵列表第一列元素的符号。假若劳斯阵列表中第一列所有元素均为正数,则该系统是稳定的,即特征方程所有的根均位于S平面的左半平面。假若第一列元数有负数,则第一列元素的符号的变化次数等于系统在S平面右半平面上的根的个数。
例3.3 系统特征方程为
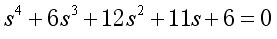
试用劳斯判据判别系统的稳定性。
解 从系统特征方程看出,它的所有系数均为正实数,满足系统稳定的必要条件。列写劳斯阵列表如下

第一列系数均为正实数,故系统稳定。事实上,从因式分解可将特征方程写为
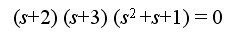
其根为-2,-3, 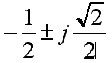 ,均具有负实部,所以系统稳定。 ,均具有负实部,所以系统稳定。
例3.3 系统特征方程为�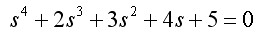
试用劳斯判据判别系统的稳定性。
�解 从系统特征方程看出,它的所有系数均为正实数,满足系统稳定的必要条件。列写劳斯阵列表如下

第一列系数有两次变号(+1到-6,-6到+5),故系统不稳定,且有两个正实部的根。
例3.4 已知系统特征方程式为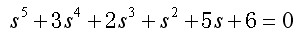
解 列写劳斯阵列表

劳斯阵列表第一列有负数,所以系统是不稳定的。由于第一列元素的符号改变了两次(5→-11→174),所以,系统有两个具有正实部的根。
4. 两种特殊情况
在劳斯阵列表的计算过程中,如果出现:
(1) 劳斯表中某行的第一列的元素为零,其余各列系数不为零(或没有其余项),或不全为零,这时可用一个很小的正数e来代替这个零,从而使劳斯阵列表可以继续运算下去(否则下一行将出现∞)。第一列零元素的存在(其他元素为正),则说明系统特征方程有一对虚根,系统处干临界状态;如果第一列元素存在符号变化,则系统不稳定,不稳定根的个数由符号变化次数决定。
例3.5 设系统特征方程为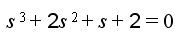
解 劳斯阵列表为
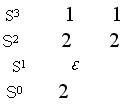
由于e的上下两个系数(2和2)符号相同,则说明有一对虚根存在。上述特征方程可因式分解为
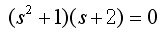
例3.5 设系统特征方程为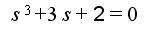
解 劳斯阵列表为
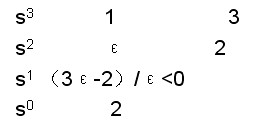
(2) 若劳斯阵列表中某一行(设为第k行)的所有系数均为零,则说明在根平面内存在一些大小相等,并且关于原点对称的根。在这种情况下可做如下处理:
a. 利用第k-1行的系数构成辅助多项式,它的次数总是偶数的;
b. 求辅助多项式对s的导数,将其系数代替第k行;
c. 继续计算劳斯阵列表;
d. 令辅助多项式等于零可求得关于原点对称的根。
例3.6 系统特征方程为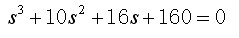
解 劳斯阵列表为

从上表第一列可以看出,各系数均未变号,所以没有特征根位于右半平面。
由辅助多项式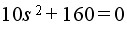 ,求得一对共轭虚根为±j4。 ,求得一对共轭虚根为±j4。
例3.7 系统特征方程式为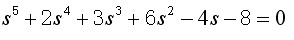
解 劳斯阵列表如下:

劳斯阵列表第一列变号一次,故有一个根在右半平面。由辅助多项式:
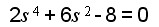
可得S1, 2 = ±1,s3, 4 = ±j2,它们均关于原点对称,其中一个根在S平面的右半平面。
(三) 劳斯判据的应用
应用劳斯判据不仅可以判别系统稳定性,即系统的绝对稳定性,而且也可检验系统是否有一定的稳定裕量,即相对稳定性。另外劳斯判据还可用来分析系统参数对稳定性的影响和鉴别延滞系统的稳定性。
 1.
稳定裕量的检验 1.
稳定裕量的检验
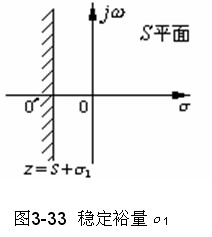
如图3-33所示,令 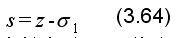
即把虚轴左移σ1 。将上式代入系统的特征方程式,得以z为变量的新特征方程式,然后再检验新特征方程式有几个根位于新虚轴(垂直线s=
-σ1 )的右边。如果所有根均在新虚轴的左边(新劳斯阵列式第一列均为正数),则说系统具有稳定裕量 σ1 。
例3.8 检验特征方程式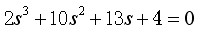 是否有根在右半平面,并检验有几个根在直线s
= -1的右边。 是否有根在右半平面,并检验有几个根在直线s
= -1的右边。
解 劳斯阵列表为

第一列无符号改变,故没有根在S平面右半平面。
再令s= z-1,代入特征方程式,得
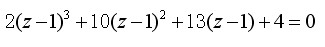
即
则新的劳斯阵列表

从表中可看出,第一列符号改变一次,故有一个根在Z平面的右半平面,即直线s= -1(即新座标虚轴)的右边,因此稳定裕量不到1。
2. 分析系统参数对稳定性的影响
设一单位反馈控制系统如图3-34所示,其闭环传递函数为

系统的特征方程式为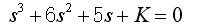
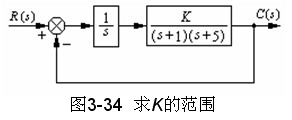
列写劳斯阵列表:
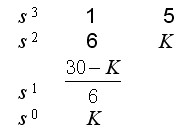
若要使系统稳定,其充要条件是劳斯表的第一列均为正数,即 K > 0, 30 - K > 0
所以0 < K < 30,其稳定的临界值为30。
由此可以看出,为了保证系统稳定,系统的K值有一定限制。但是为了降低稳态误差,则要求较大的K值,两者是矛盾的。为了满足两方面的要求,必须采取校正的方法来处理。
例3.9 系统特征方程式为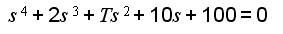
求系统稳定时,参数T的范围?
解 劳斯表为

由劳斯表可以看出,要使系统稳定,必须
 即T
> 25时,系统稳定。 即T
> 25时,系统稳定。
|

