(二)极坐标图法
在GH平面上作出系统的开环频率特性的极坐标图,并作一单位圆,由单位圆与开环 频率特性的交点与坐标原点的连线与负实轴的夹角求出相角裕度γ;由开环频率特性与负轴交点处的幅值 频率特性的交点与坐标原点的连线与负实轴的夹角求出相角裕度γ;由开环频率特性与负轴交点处的幅值
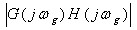 的倒数得到幅值裕度Kg。 的倒数得到幅值裕度Kg。
在上例中,先作出系统的开环频率特性曲线如图 4-55所示,作单位圆交开环频率特性曲线于A点,连接 OA,射线OA与负实轴的夹
角即为系统的相角裕度γ=80度。开环频率特性曲线与负实轴的交点坐标为(0.8,j0)
由此得到系统的幅值裕度 Kg=1/0.8=1.25
(三)伯德图法
画出系统的伯德图,由开环对数幅频特性与零分贝线(即ω轴)的交点频率ωc,求出对应的相频特性与-180度线的相移量,即为相角裕度
γ。 当对应的相频特性位于 –180度线上方时,γ> 0度;反之,当ωc对应的相频特性位于 –180度 线下方时,
γ< 0度。 然后,由相频率特性与-180度线的交点频率ωg ,求出对应幅频特性与零分
贝线的差值,即为幅值裕度Kg的分贝数。当ωg对应的幅频特性位于零分贝线下方时, ,Kg > 0dB反之,当 对应的幅频特性位于零分贝线上方时,Kg
> 0dB 。
 例5—9的伯德图如图4-56所示。从图中,可直接得到幅值穿越频率ωc=2,
相角穿越频率ωg=5,相角裕度γ≈80度,幅值裕度Kg =2dB。 例5—9的伯德图如图4-56所示。从图中,可直接得到幅值穿越频率ωc=2,
相角穿越频率ωg=5,相角裕度γ≈80度,幅值裕度Kg =2dB。
比较上述三种解法不难发现:
解析法 比较精确,但计算步骤复杂,而且对于三阶以上的高阶系统,用解析法是很困难的。
图解法 以极坐标图和伯德图为基础的图解法,避免了繁锁的计算,具有简便、直观的优点,对于高阶系统尤为方便。不过图解法是一种近似方法,所得结果有一定误差,误差的大小视作图的准确性而定。伯德图法和极坐标法虽然都是图解法,但前者不仅可直接从伯德图上获得相角裕度
γ和幅值裕度Kg,而且还可直接得到相应的幅值穿越频率ωc 和相位穿频率ωg 。同时伯德图较极坐标图方便,因此在工程实践中得到更为广泛的应用。
四、稳定裕度与系统的稳定性
前面我们已经介绍,求出系统的稳定裕度可以定量分析系统的稳定程度。下面我们通过两个示例进一步说明。
例4-10 已知最小相位系统的开环传递函数为

试分析稳定裕度与系统稳定性之间的关系。
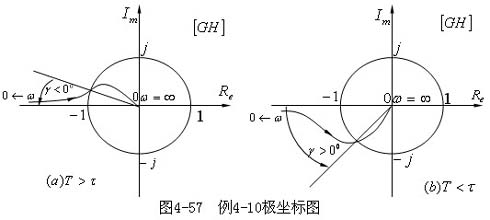
解 该系统的开环频率特性的极坐标图分别如图4-57(a)(当T>τ 时)和 图4-57(b)(当T<τ时)所示。由
图4-57(a)可知,当T>τ 时,系统的相角裕度γ<0 ,由图4-57(b)可知,当T>τ 时,系统的相角裕度γ>0
。系统的幅值裕度用解析法求解如下:
系统的幅频特性和相频特性分别为
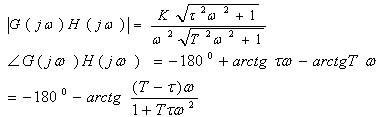
令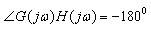 ,则有
,则有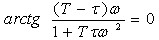 , 故 ωg=0 或 ωg=∞对应S平面的坐标原点,舍去ωg=∞(T≠τ)。 ,由此求出系统的幅值裕
, 故 ωg=0 或 ωg=∞对应S平面的坐标原点,舍去ωg=∞(T≠τ)。 ,由此求出系统的幅值裕
度为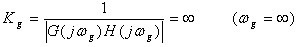 。可见,当ωg=0,则Kg=∞>1
当T>τ时,γ<0 ,该系统不稳定; 。可见,当ωg=0,则Kg=∞>1
当T>τ时,γ<0 ,该系统不稳定;
当T<τ时,γ>0 ,该系统是稳定的,结论与例4-8应用奈氏判据的结果一致。
例4-11 已知非最小相位系统的开环传递函数为
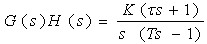
试分析该系统的稳定性及其与系统稳定裕度之间的关系。
 解
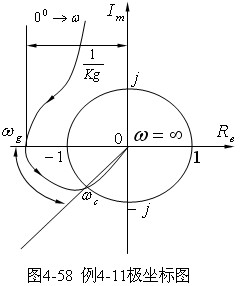
在一定的K值条件下,系统的开环频率特性如图4-58所示。由于该系统有一个为于右半部S平面的开环极点(p=1) ,奈氏曲线逆时针包围(-1,j0)点一周(N=-1),根据奈氏判据,该系统为稳定系统。 解
在一定的K值条件下,系统的开环频率特性如图4-58所示。由于该系统有一个为于右半部S平面的开环极点(p=1) ,奈氏曲线逆时针包围(-1,j0)点一周(N=-1),根据奈氏判据,该系统为稳定系统。
但由图解法求出该系统的相角裕度γ>0 ,幅值裕度Kg<1,这说明以相角裕度γ>0 和幅值裕度Kg>1作为判别非最小相位系统稳定性的依据是不可靠的。
从上面示例可以看出,对于非最小相位系统,不能简单地用系统的相角裕度和幅值裕度的大小来判断系统的稳定性。但对于最小相位系统以相角裕度γ>0和幅值裕度Kg>1(或
K(dB)>0)作为系统稳定的充要条件是可靠的。
|

